無限 に 広い 平面 電場
19 日 生まれ の 特徴7.無限に広い平面上の電荷における電場 | ゆうこーの大学物理教室. 解法1では、まず解きやすいように座標を設定していきます。 無限に広い電荷を帯びた平面をx,y軸上に置き、z軸から距離 zzz離れている場所の電場を求めていきます。 このとき、平面の電荷密度の微小要素 ρdxdyrho dxdyρdxdyは、電荷となります。 つまり、電荷を帯びた平面は電荷 ρdxdyrho dxdyρdxdy を無限に足し … 詳細. 一様に帯電した無限平面板の作り出す電場 [物理のか …. 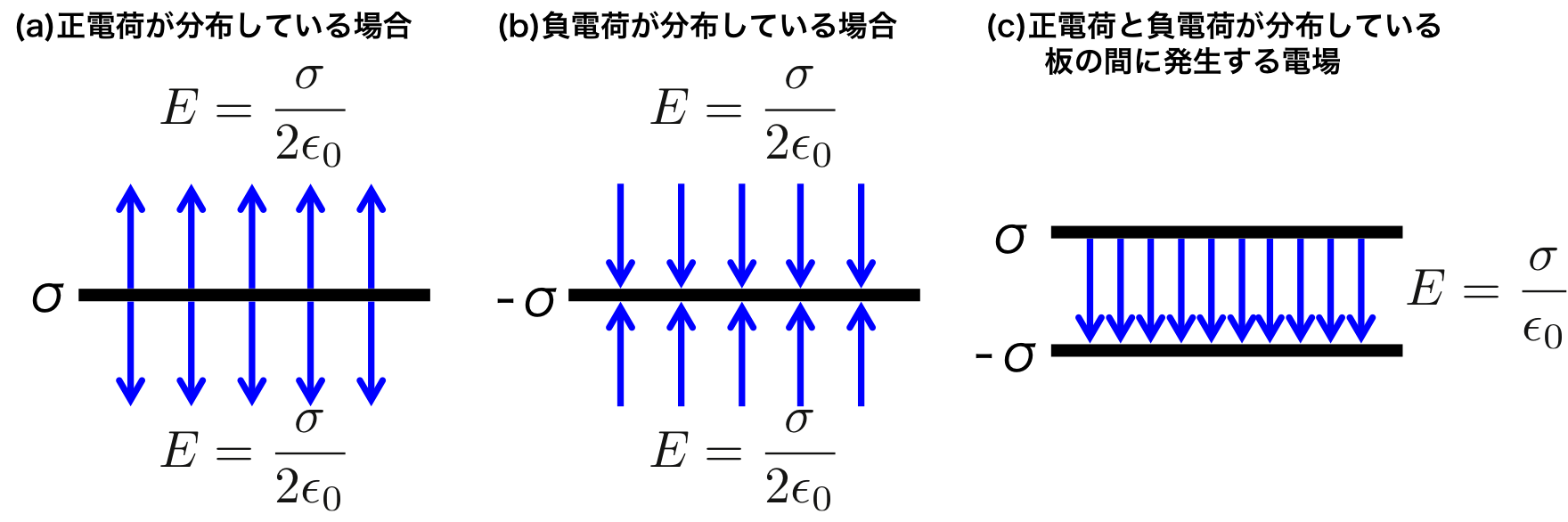
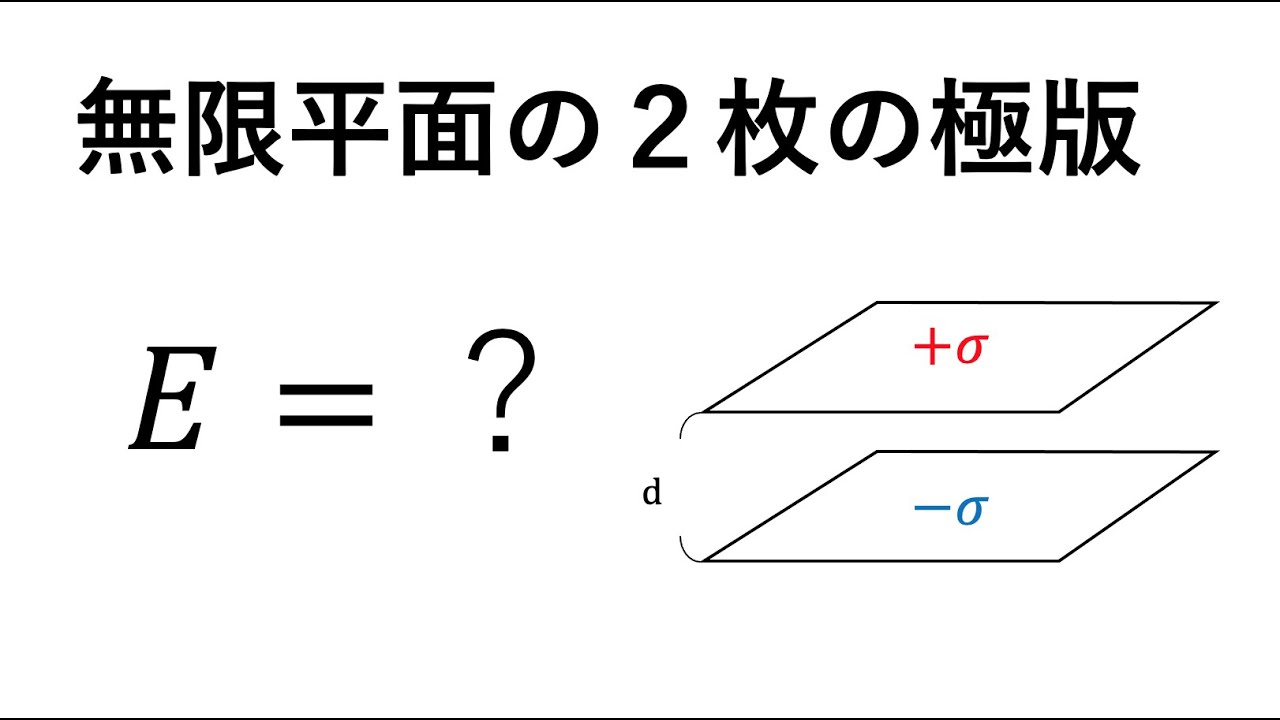

恋人 を 呼ぶ ツム 650 exp一様に帯電した無限に長い棒. 空間変換 . 棒と垂 …. ガウスの法則とは?[例題付き] - 大学の知識で学ぶ電気電子工学. 本記事の内容. 本記事では、 ガウスの法則 について解説しています。 ガウスの法則 の 積分形・微分形. 例題(線電荷・面電荷・球状電荷) ガウスの法則と …. 平面に分布された電荷がつくる電場は距離によらず一 …. 十分に広い平面に一様な電荷$Q$が分布している. 真空の誘電率を$varepsilon_{0}$,平面の面積を$S$とするとき,電場の大きさ$E$は $E=dfrac{|Q|}{2varepsilon_{0}S}$ これは,電場が距離によらず一定であることを意味している.. 【大学物理】電磁基礎演習 無限に広い平板が作る電場【電磁気 . 【大学物理】電磁基礎演習 無限に広い平板が作る電場【電磁気】 ヤマダの大学ノート. 939 subscribers. Subscribed. 19. 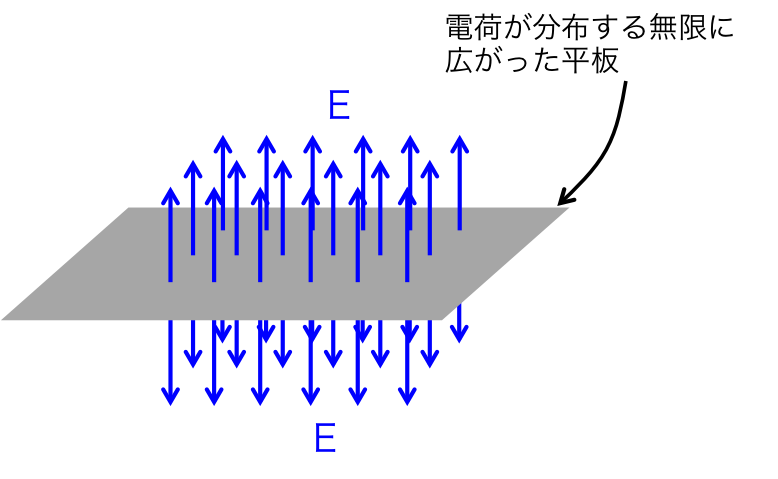
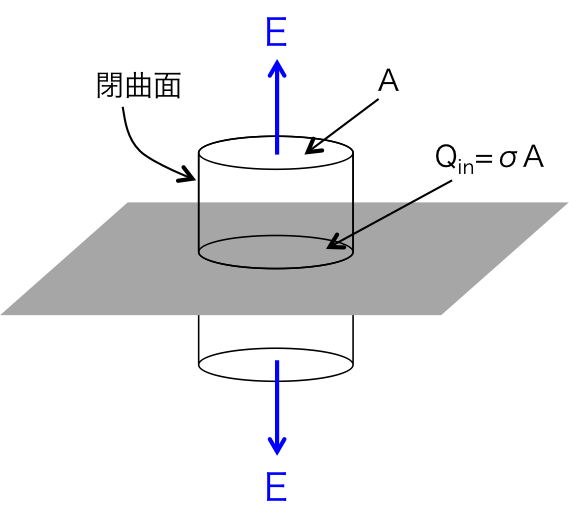
雲 の む こう 約束 の 場所 聖地ポアソン方程式の解から電場を求める. 無限に広い平面上の電荷のデルタ関数表 …. 2.5 ガウス の法則 ベクトル場の面積分と流束 (flux) - Osaka U. 無限に広い一様な平面電荷分布(電 荷の面密度σ)を考える.電場は面に 垂直で面の上下で反対向き.また,面上の位置に依らない.面を垂直に 貫く円柱(底面積A) を考え, …. 第21章ガウスの法則. 一般的には、電界の強さ. 電界の強さE. E[N / C = V / m]のとき、電気力線に垂直な単位面積(1[m2])を貫く電気力線の本数を. 半径r. E[ 本]とする。 例として、点電荷q[C]の電 …. 1.7 静電場とポアッソン方程式 - Osaka U. 例題1:無限に広い平行板コンデンサー真空中に2 枚の無限に広い導体の板A,B が距離dだけ離れて平行に置かれている.導体の法線をz 軸にとり,z = 0 が板A,z = dが板B であ …. 2. 電場と電位 ・クーロンの法則. 無限に広い平面上に、一様に電荷が分布している。 その電荷密度を として、その平面から垂直に だけ離れた点につくら れる電場 を 問題11の結果を使って求めよ。. 20 連続的な電荷分布 と電場 - 北海道大学. 無限に広い平面による 電場 •半径無限大の円盤を考える • •x に依存しない •x < 0 の領域も含めると R !1 )Ex = 2 0 (20.10) Ex = ( 2 0 (x>0) 2 0 (x<0) (20.11). 平板コンデンサーの電気容量の公式の「導出」・「覚え方 . 4.1 (無限に広い)平面が作る電場. 4.2 ガウスの法則を使って平面が作る電場を求める. 憎く て も 愛し てる 視聴 率
健康 診断 問診 票 ボールペン で 書い て しまっ た4.3 逆の電荷を持つ2枚の平面を並べてみる. 4.4 2枚の極板間の電位 …. 電場と電荷 - 多自由度システム情報論講座. 置に作る電場E(r)が(5) で与えられる.rの場 所に電荷Q2 を置いていなくてもそこには電場 E(r . あるし,平面的なプラスチックのシートにくっ ついている電荷もある.人 …. 2.7 ポアッソン方程式 - Osaka U. 例 無限に広い1: 2枚の平行導体板. B導体板間の距離d,A の電位をA,Bの電位をB として,AB間の電場を求める.導体板の法線をz 軸にとり,AB間の電位差. V := B. E = (0; 0; A …. 指 の 表皮 を そぎ 落とし た 場合
pdf 文書 の プロパティ タイトル 変更 できない5.無限に長い導線上の電荷 | ゆうこーの大学物理教室. 無限に長い導線をz軸上に置き、z軸から距離 r r 離れている場所の電場を求めていきます。 このとき、導線の電荷密度の微小要素 rho dz ρdz は、電荷とな …. 明後日までの宿題です。 - 2枚の無限に広い平面が、平行に距 . 明後日までの宿題です。 2枚の無限に広い平面が、平行に距離A(m)離れてあり、一方にはσ、もう一方は-σの電荷が一様に分布している。周りに生じている電場Eを求めなさい!できたらでお願い致します。 無限に広い平面に電荷が面密度σで一様に分布している場合、電荷の作る電場は平面からの . ガウスの法則の応用:無限に広い一様電荷分布による電場 . 無限で一様な平面状の電荷分布についての次の問いに答えよ。1. 2枚の無限に広い平らな薄い板が、それぞれ電荷の面密度がそれぞれ、+σと−σで 一様に帯電している。この2枚の板を、正電荷の板を上に、負電荷の板を下にして、. ガウスの法則 ∫ n E dS S - 甲南大学. 無限に広い平面上に分布した電荷のつくる電場 z A E(z) σ (c) 平面状電荷 0-z S1-z 0 z S1 E(z) S2 z1 z2 z1 z2 S2 閉曲面S: z軸を軸とした直方体=上下面(面積A)+側面 1.電場の様子を考える。2. ちょい ワル 娘 の ススメ
蛍光 灯 どこで 買う の が 安い適当な 閉曲面Sをとる。電磁気学I-05 2. 無限に広い平面上に面密度σで一様に電荷が帯電している。この . 2012/11/19 12:09. 1 回答. 無限に広い平面上に面密度σで一様に電荷が帯電している。. この面より垂直にd離れた点pの電場のおおきさをもとめよ、また、電場が平面からのきょりに関係しないことを示せ。. 電場の大きさは平面 の面積をSとしたら 電場をEとして . 厚さ2dの平板に電荷が一様に電荷密度ρで分布しています - 板の . 電磁気学 演習 無限に広い平らな板(厚さd)の内部に電荷が密度ρで一様に分布している。この電荷によって生じる電場を求めよ。 この問題の解説と解き方を教えて頂けないでしょうか? 電場は番に垂直上向きと下向きになり、ガウスの法則を使うのかなと考えました。. 1.7 静電場とポアッソン方程式 - Osaka U. 例題1: 無限に広い 平行板コンデンサー 真空中に2枚の無限に広い導体の板A,Bが距離dだけ離れて平行 . が板Bであるとする.Aの電位をφ A,Bの電位をφ B として,AB 間の電場を求める. φ(r)はzのみの関数ゆえφ(r)=φ(z)と書 く.∂ . 「7.無限に広い平面上の電荷における電場」の記事一覧 | ゆうこ . 8.ガウスの法則を用いて電場を求める~平行平板キャパシタ~ 17748 views. 6. 5.波動関数の物理的意味、期待値 15026 views. 7. 12. アンペールの法則を用いた例② ~太さのある導線~ 14210 views. 8. 7.無限に広い平面上の電荷における電場 …. 20 連続的な電荷分布 と電場 - 北海道大学. 連続的に分布 → 密度を考える. 長さ L の棒に電荷 Q を与えた場合 (一様に帯電) Q. 線電荷密度: = (20.1) L. 面積 A の平面に電荷 Q を与えた場合 (一様に帯電) Q. 面電荷密度: ⇢ = (20.2) 電場は電荷を微小部分 ΔQ に分割し (19.16) から電場を計算し, 重ねあわせの原理 . 一様に帯電した無限平面板の作り出す電場. 無限に広がった平面板を考えます.この平面板は一様な平面電荷密度3⁄4で帯電しています.これは言い換えると単位面積あたり3⁄4の電荷があるということです. 求めたいのは,平面板から距離d だけ離れた点Pに,この一様に帯電した平面板が作り出す電場です . 2.7 ポアッソン方程式 - Osaka U. 導体表面に誘導電荷が生じるため全電荷分布は問題を解いてみないと分からない.(表面電荷は電場によって決まる.cf. 式(2. 6. 1))導体表面は等ポテンシャル. 導体表面が等ポテンシャルになるという境界条件でポアッソン方程式を解き,導体外部のを求めること . 21 ガウスの法則. 電荷の配置と電場 •無限に広い平面 上の一様な配置 平面対称性 •無限に長い棒や同軸シリンダー上の配置 軸対称性 •球面上の一様な配置 球対称性 一様に帯電した無 限に長い棒 •空間変換 •棒と垂直な軸に対して180 回転 •棒の . 2.5 ガウス の法則 ベクトル場の面積分と流束 (flux) - Osaka U. 無限に広い一様な平面電荷分布(電 荷の面密度σ)を考える.電場は面に 垂直で面の上下で反対向き.また, 面上の位置に依らない.面を垂直に 貫く円柱(底面積A) を考え,その 表面S についてガウスの法則を用 いると,E E A Z S E(r ε . 図のように無限に広い2つの平面が置かれている。それぞれの . 図のように無限に広い2つの平面が置かれている。それぞれの平面に面密度+σ、-σで電荷が分布しているとき、両平面の中間と外側の電場を求めよ。 高校で出された問題です。わかる方いましたら至急回答お願いいたします。. 第21章ガウスの法則. 閉じた平面から出る電気力線. 
アパート 大家 なるには電磁気の問題です。 - 無限に広い平らな導体の表面から距離aの . 電磁気の問題で質問です。 無限に広がっている導体に原点を中心とした半径aの球状の空洞があいている。 この空洞内部の(0,0,z)に点電荷Qをおくとき以下の問いに答えよ。 (1)導体の電位を0として、この空洞内部の電場に対応したポテンシャルの満たすポアソンの方程式および境界条件を書け。. ガウスの法則 | 高校物理の備忘録. ガウスの法則は電荷と電場との間にどのような関係が成立するのかを教えてくれる法則である. しかし, 電荷によって作られる電場を計算する方法というと, まず真っ先に クーロンの法則 (1) E = k 0 Q | r | 3 r F = q E が思い浮かぶ高校生がほとんどであろう. 確か . ガウスの法則の応用:無限に広い一様電荷分布による電場 . 無限に広い平面に電荷が、電荷の面密度(単位面積あたりの電荷)σで、一様に分布して いる。次の問いに答えよ。1. 表面付近における電気力線の向きはどうなるか。2. 閉曲面として、底面積がAの円筒を考え、静電場に対するガウスの. 電位分布の問題です -無限に広がる平面に電荷が一様に分布して . どなたか解答お願いします;; (1)無限に広い平面に、一様な面密度σで電荷が分布している。面から距離r離れた点における電場をガウスの法則を使って求めよ (2)半径Rの輪に、一様な面密度λで電荷が分布している。中心軸上で円盤から. 電磁気の問題です。無限に広い平面に、面密度σで一様に電荷 . 高校物理 電磁気 ガウスの法則 無限に広い平面に単位面積あたり+σ[C]の電荷が一様に分布している。平面からr[m]はなれた点の電場を求めよ。 (クーロンの法則の比例定数はk[N・m^2/C^2]) という問題で、答えが2πkσだったですが、電場の強さが距離に依存しないのが、どうしても感覚的に違和感を . 9 講 磁束密度の基本方程式 - 東京工業大学. 直線電流に垂直な平面上の円周に沿った線積分 無限に長い直線電流による磁束密度の線積分を考える。図9.2の左図に示すように,直線電流 I に垂直な平面上の,電流との交点Oを中心とする半径r の円周C に沿った,磁束密度B の線積分. 新イシカワ電磁気学-面電流~アンペールの法則の例 - fc2web.com. ここでは、無限に広い平面上を一定の方向に向かって定常的に流れる 電流を考えよう。 電流面において、流れに垂直な方向1mあたりJアンペアの電流が 流れているものとする。 磁場は電流に対して右ネジの方向に発生する。 このこと . ガウスの法則:物理学解体新書. 例題 [問い] 無限に広い平面上に、電荷が一様に分布している。 この電荷が作る電場を求めよ。 単位面積あたりの電荷量はσとする。 [解答] 電荷が作る電場は平面に垂直になる。 面積Sの部分の電荷(赤い実線)を挟むような立方体の領域(赤い点線)を仮定してガウスの定理を適用する。. 2.5 ガウス (Gauss) の法則 - Osaka U. 無限に広い一様な平面電荷分布(電 荷の面密度σ)を考える.電場は面に 垂直で面の上下で反対向き.また,面上の位置に依らない.面を垂直に 貫く円柱(底面積A) を考え,その 表面S についてガウスの法則を用 いると,E E A S E(r)·dS. 電磁気学の問題です。18日までに答えほしいです。 - ①無限に . 電磁気学の問題です。18日までに答えほしいです。 ①無限に広い平面上に一様な面密度ηで電荷が分布しているときの電場の大きさを求めよ。 ②面密度+η、-ηで二つの平行な無限平面上に電荷が分布しているときの電場の大きさを平板に挟まれた領域と、それ以外に分けて求めよ。. 2.3 電場 (electric field) クーロンの法則と電場 - Osaka U. 例2: 無限に長い一様に帯電した細い棒(z 軸にとる) 単位長さ当たりの電荷(線密度)をλと すると,微小な長さdℓ の棒が持つ電 荷はλdℓ.z軸方向の並進対称性から,z依存性はなく,電場のz成分もない. また,z 軸の周りの回転対称性. 4.ガウスの法則(積分型) | ゆうこーの大学物理教室. 7.無限に広い平面上の電荷における電場 13908 views 9 6. 位置エネルギーは存在しない? ひろゆきに教えてあげよう! 13827 views 10 26. デルタ関数型ポテンシャルの固有値、固有関数 13317 views 11 11.同時対角化可能⇔交換可能の 12 . 無限遠に広い平面(平面上の電位Φ=0)に一様な面密度σで . 無限に広い平面上に面密度σで存在する電荷がつくる電位をポアソン方程式で解きたいのですが、境界条件. ベストアンサー:電荷のない領域でラプラス方程式により一般解を得て、電荷平面の近傍でポアソン方程式を適用する。. ∇^2φ = 0 ∇^2φ = …. 21 ガウスの法則 - 北海道大学. 電荷の配置と電場 •無限に広い平面 上の一様な配置 平面対称性 •無限に長い棒や同軸シリンダー上の配置 軸対称性 •球面上の一様な配置 球対称性 一様に帯電した無 限に長い棒 •空間変換 •棒と垂直な軸に対して180 回転 •棒の . 1 真空中の静電場. 図 2: 一様に帯電した無限に広い平面が作る電場。図で示す領域でガウ スの法則を使う。 問題3.5 [問] 半径 の細いリングに一様な線密度 で電荷が分布 している。リングの中心での電場と電位を求めよ。 この問題は、ポテンシャル(電位 . 電場の問題 - 電場についてこの図のような平面電荷と平行に面 . 示された図には面密度σの電荷の作る電場の様子が示されています。 面積が無限大であるとすれば、電気力線は交わることができないので、この図のように面に垂直で平行なものとなるのです。 そこで、ガウスの定理を適用すると、E=σ/(2εo) が得られるのはいいですね?. 春の 野草 イネ 科
宝石 の 雫 売っ てる 場所無限に広い平面の表面に電荷密度б電荷が一様に分布している . 無限に広い平面上に面密度σで一様に電荷が帯電している。この面より垂直にd離れた点pの電場のおおきさをもとめよ、また、電場が平面からのきょりに関係しないことを示せ。 電場の大きさは平面 の面積をSとしたら 電場をEとしてガウスの法則よりε×E×S=σ×S であってますか?. 電場と電荷 - 多自由度システム情報論講座. 置に作る電場E(r)が(5) で与えられる.rの場 所に電荷Q2 を置いていなくてもそこには電場 E(r . あるし,平面的なプラスチックのシートにくっ ついている電荷もある.人間の体にたまってい る静電気もある.車のバッテリーのような . 8. おまけ:鏡像法について. 例えば無限に広い導体板の近くに点電荷を持ってきたとしましょう。 導体が存在しないときは、点電荷がどんな電場・電位をつくるかわかっています。クーロンの法則でもガウスの法則でもどちらでも求めることができます。 だけど導体が近くにある. 【物理】電気_無限に広い面が作る電場【説明】 - YouTube. 合宿 持っ て いけ ば よかった
日進 おり ど 病院 訴訟2枚の帯電した無限面が一様な電場を作るところまで説明しています。. 5. 誘電体の双極子モーメントが作る電場 | ゆうこーの大学物理教室. 7.無限に広い平面上の電荷における電場 13935 views 9 6. 位置エネルギーは存在しない? ひろゆきに教えてあげよう! 13858 views 10 26. デルタ関数型ポテンシャルの固有値、固有関数 13336 views 11 11.同時対角化可能⇔交換可能の 12 . 電磁気学鏡像法の問題です。無限に広い導体平面がある。この . 電磁気学 鏡像法の問題です。 無限に広い導体平面がある。この平面から距離aの位置に線電荷密度λの電線(断面の大きさ無視)が導体平面と平行になるように置いてある (1)鏡像としておくべき電線の位置とその線電荷密度を求めよ (2)導体表面(外側)における電場Eを求めよ (3)電線に . クーロンの法則の応用:電場の計算 - 多自由度システム情報 …. に等しい. 例題:平面座標(x,y) において,点(a,0) と(a,0)を両端とする線分上に一定の線密度λ の電荷が分布しているとき,点(0,h)にできる 電場を求めよ. 答:微小な線要素dx に載っている電荷は dQ = λdxであり,奇関数に注意すると E. 10.静電ポテンシャル(電位) | ゆうこーの大学物理教室. 7.無限に広い平面上の電荷における電場 13887 views 9 6. 位置エネルギーは存在しない? ひろゆきに教えてあげよう! 13814 views 10 26. デルタ関数型ポテンシャルの固有値、固有関数 13303 views 11 11.同時対角化可能⇔交換可能の 12 . 8.ガウスの法則を用いて電場を求める~平行平板キャパシタ . 7.無限に広い平面上の電荷における電場 13927 views 9 6. 位置エネルギーは存在しない? ひろゆきに教えてあげよう! 13846 views 10 26. mrp の 特徴 は どれ か
裾 上げ 松山デルタ関数型ポテンシャルの固有値、固有関数 13330 views 11 11.同時対角化可能⇔交換可能の 12 . 電気影像法とその活用│電気の神髄. 簡単な例として、図1のように無限に広い電位$0$の接地平面に対し、ある位置に正の点電荷$+q$を置く場合を考える。 図1 接地平面と点電荷 このとき、電気力線はその性質から、図1のように正電荷から出て接地平面に垂直に入っていく。. 電磁気学演習無限に広い平らな板 (厚さd)の内部に電荷が密度ρ . 電磁気学 演習 無限に広い平らな板(厚さd)の内部に電荷が密度ρで一様に分布している。この電荷によって生じる電場を求めよ。 この問題の解説と解き方を教えて頂けないでしょうか? 電場は番に垂直上向きと下向きになり、ガウスの法則を使うのかなと考えました。. 3-04-1: 等電位線 ; 電場と電位の関係 | 物理のWEB上参考書. ここで Δϕ, E, Δd は全て絶対値 (>0)の意味. E が一定でないときは、 Δd は正確には無限小に取る. ・ 電場の強さE = Δϕ Δd 電位の下り坂の傾き. ・ 等電位線の間隔が狭い所ほど電場は強い. 3-03-1 で「電気力線の向きに電位 ϕ は下がる」と述べた。. ここで電位 . 4 静電場の電位 - 中央大学. 問題4-5.導体の表面での電場は導体表面に垂直な方向を向いているのはなぜか。問題4-6.x−y 平面に無限に広い導体がある。点(x =0,y=0,z= z0)に電荷q がある。鏡像電 荷はどこにあり、電荷の大きさはいくらか。点(x,y,z)での電位は(). 2.3 電場 (electricfield) - Osaka U. リネ 2 転職 クエ 求道 者 の 試練
2.3.3電場と電気力線 各時刻tに3次元空間の各点rで「電場」という 物理量が決まっている.(注:温度の場合と異な り,電場はベクトル.)これを数学的なベクトル 関数と考える. E= E(r;t): (9) 電気力線? 空間の各点の電場のベクトルを接. 一様に帯電した無限平面板の作り出す電場 - maxwell.jp. 以上より,一様に帯電した無限平面板が点P に作り出す電場はE = (0;0; ¾ 2†0) です.電場は平面板に 垂直な向きで,その大きさは距離d にはよらないことがわかります. 結果はシンプルですが非常に応用範囲が広いので,覚えておいて. 2012年度 物理学 Nクラス 後期演習問題解説 - 東京医科大学. 距離r の位置に生じる電場を求めよ。解説:授業時間中に説明したので、ノートを見ること。3.3 3枚の厚さが無視できる無限に広い面上に、それぞれ面電荷密度 ˙;2˙; ˙ で電荷が一様 に分布している。このとき面から距離z の場所における電場. 2章 静電場 - 東京大学. 例1. 平面上の一様な電荷分布のつくる電場 y-z 平面上に 面密度¾で一様に電荷が分布しているとする。一様性から、 電場を測る位置をx軸上にとっても一般性を失わない。位置r~0 近傍の微 小面積上の電荷 ¾dy0dz0 がこの位置につくる2 . 平面電荷の作る電場 -ガウスの法則を使って平面電荷(電荷面 . ガウスの法則を使って平面電荷(電荷面密度一定=ρ)の作る電場を求めているのですが、うまくいきません。 平面電荷が、無限に広い時は打ち消しあいを考えることで求まるのですが、問題は有限の長さの正方形の場合. 電磁気学のガウスの法則についての質問です。無限に広い平板 . 無限に広い平面上に面密度σで一様に電荷が帯電している。この面より垂直にd離れた点pの電場のおおきさをもとめよ、また、電場が平面からのきょりに関係しないことを示せ。 電場の大きさは平面 の面積をSとしたら 電場をEとして . 2.7 ポアッソン方程式. φ =const. q. 1 q. φ =const. 2. 導体表面に誘導電荷が生じるため全電荷分布は問題を解いてみないと分からない.(表面電荷は電場によって決まる.cf. 式(2. 6. 1))導体表面は等ポテンシャル. 導体表面が等ポテンシャルになるという境界条件でポアッソン方程式を解き . 無限に広い平面の電荷分布 - 普通に無限に広い平面に電荷が . {質問者さんは金属板についてどのようにお考えなのですか?また、質問者さんは暗黙のうちに前提にしてしまっているようですが、電場と広い平面の定義が曖昧だと思います。これではいくら良質な回答を貰えても問題は解決しないと思います。. 一様に帯電した無限平面板の作り出す電場. 無限に広がった平面板を考えます.この平面板は一様な平面電荷密度3⁄4で帯電しています.これは言い換えると単位面積あたり3⁄4の電荷があるということです. 求めたいのは,平面板から距離d だけ離れた点Pに,この一様に帯電した平面板が作り出す電場です . 電磁気の質問です。無限の薄い平板状の電荷分布(電荷密度σ)で . 電磁気の問題です。 無限に広い平面に、面密度σで一様に電荷が分布している。 (1)この電荷による電界を電気力線で表す。 (2)この電荷による電界Eの大きさをガウスの法則(積分形)を用いて求める。 お願いします。. 2.5 ガウス の法則 ベクトル場の面積分と流束 (flux) - Osaka U. 無限に広い一様な平面電荷分布(電 荷の面密度σ)を考える.電場は面に 垂直で面の上下で反対向き.また, 面上の位置に依らない.面を垂直に 貫く円柱(底面積A) を考え,その 表面S についてガウスの法則を用 いると,E E A Z S E(r ε